Hey there, I’ve got a question for you.

With only gravity to move you, what is the fastest way to roll or slide from a point A to some other point B below(but not directly below):

1. Would it be a straight line – AB?
2. Or some other path?

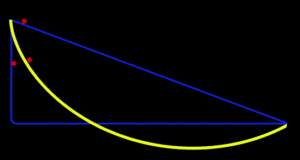
Straight Line between A and B would certainly be the shortest path but what if I told you – this shortest path does not take the least time to travel between points A and B? Surprised, huh?
To get to know about the reason and the answer to this question, we’ll have to jump right into the time machine. Let’s go.

History of Brachistochrone

A Question for the world

Johann Bernoulli asked this question to the readers of Acta Eruditorum (a Scientific Journal) in June 1956.
He posed the problem of Brachistochrone as a challenge to the world’s most brilliant mathematicians to gain the gratitude of the whole scientific community as he believed that this problem would test their methods and strength of their intellect.
Bernoulli wrote the problem statement as:

Given two points A and B in a vertical plane, what is the curve traced out by a point acted on only by gravity, which starts at A and reaches B in the shortest time.

Johann and his brother Jakob Bernoulli derived the same solution, but Johann’s derivation was incorrect and he tried to pass off Jakob’s solution as his own. His derivation of the differential equation for the curve yielded a Cycloid but the use of only a single constant marred his proof.

A Lion and his Claw

Bernoulli didn’t receive the solution for the first six months and extended the time for submissions for another year and a half on Leibniz’s request.
On 29 January 1697, Isaac Newton found the challenge in a letter from Johann Bernoulli. He stayed up all night to solve it and mailed the solution anonymously by the next post.
Bernoulli immediately recognized the author and exclaimed that he “recognizes a loin from his claw mark“. This story gives some idea of Newton’s power, since Johann Bernoulli took two weeks to solve it.
Newton also wrote, “I do not love to be dunned [pestered] and teased by foreigners about mathematical things…“.

Solution by Johann Bernoulli

In March 1697, Johann Bernoulli stated that he had found two methods (always referred to as “direct” and “indirect”) to show that the Brachistochrone was the “common cycloid”, also called the “roulette”.

An attempt on Brachistochrone before Bernoulli

Earlier, in 1638, Galileo had tried to solve a similar problem for the path of the fastest descent from a point to a wall. He draws the conclusion that the arc of a circle is faster than any number of its chords.
Although, Galileo warned of possible fallacies and the need for a “higher science”. The actual solution to Galileo’s problem is half a cycloid. Galileo studied the cycloid and gave it its name, but the connection between it and his problem had to wait for advances in mathematics.

So, what exactly is… Brachistochrone?

So, which path between points A and B would take the least time?
Straight line between A and B would certainly be the shortest path but when you fall, gravity accelerates you and falling vertically a lot right away would mean having top speed during more of the journey.
Hence, Brachistochrone curve is the path with least time to travel from point A to point B below(not directly below). The term Brachistochrone means Shortest time.

Brákhistos(Shortest) khrónos(Time)

Johann’s Solution – Indirect Method

According to Fermat’s principle, the actual path between two points taken by a beam of light is one that takes the least time.

In 1697 Johann Bernoulli used this principle to derive the brachistochrone curve by considering the trajectory of a beam of light in a medium where the speed of light increases following a constant vertical acceleration (that of gravity g).

What is a Tautochrone?

Brachistochrone curve also holds true – an interesting property, that of a Tautochrone Curve.
So, what is a Tautochrone Curve?
A tautochrone or isochrone curve (tauto- same or iso- equal, and chrono time) is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve.

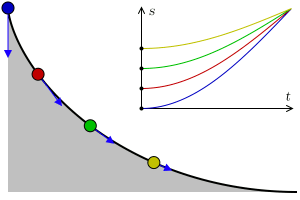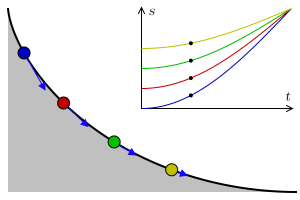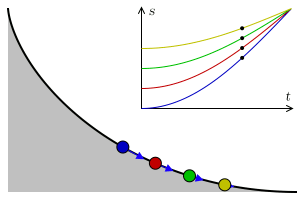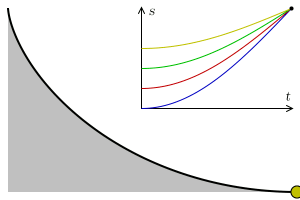
Four balls slide down a cycloid curve from different positions, but they arrive at the bottom at the same time. The blue arrows show the points’ acceleration along the curve. On the top is the time-position diagram.

Verdict

Next time I hop onto a slide, I’ll go via a Brachistochrone to reach the bottom in the least time. I hope not to hurt myself while doing it. 🤨